Grupo poliédrico

Grupos de puntos en tres dimensiones

Simetría involutiva Cs, (*) [ ] =	Simetría cíclica Cnv, (*nn) [n] =	Simetría diédrica Dnh, (*n22) [n,2] =
Grupo poliédrico, [n,3], (*n32)
Simetría tetraédrica Td, (*332) [3,3] =	Simetría octaédrica Oh, (*432) [4,3] =	Simetría icosaédrica Ih, (*532) [5,3] =

En geometría, un grupo poliédrico (o también grupo poliedral) es cualquiera de los grupos de simetría correspondiente a alguno de los sólidos platónicos.^[1]​

Grupos

Hay tres grupos poliédricos:

• El grupo tetraédrico de orden 12, el grupo de simetría rotacional del tetraedro regular. Es isomorfo a A₄.
  • Los conjugados de T son:
    • La identidad
    • 4 × rotación de 120°, orden 3, en sentido horario
    • 4 × rotación de 120°, orden 3, en sentido antihorario
    • 3 × rotación de 180°, orden 2
• El grupo octaédrico de orden 24, grupo de simetría rotacional del cubo y el octaedro regular. Es isomorfo a S₄.
  • Las clases de conjugación de O son:
    • La identidad
    • 6 × rotación de ±90° alrededor de los vértices, orden 4
    • 8 × rotación de ±120° alrededor de los centros de los triángulos, orden 3
    • 3 × rotación de 180° alrededor de los vértices, orden 2
    • 6 × rotación de 180° alrededor de los puntos medios de las aristas, orden 2
• El grupo icosaédrico de orden 60, grupo de simetría rotacional del dodecaedro regular y el icosaedro regular. Es isomorfo a A₅.
  • Las clases de conjugación de I son:
    • La identidad
    • 12 × rotación de ±72°, orden 5
    • 12 × rotación de ±144°, orden 5
    • 20 × rotación de ±120°, orden 3
    • 15 × rotación de 180°, orden 2

Estas simetrías se duplican a 24, 48 y 120 respectivamente para los grupos reflexivos completos. Las simetrías de reflexión tienen 6, 9 y 15 planos de reflexión respectivamente. La simetría octaédrica, [4,3] puede verse como la unión de 6 planos de reflexión de simetría tetraédrica [3,3] con 3 otros planos de reflexión del grupo diédrico Dih₂, [2,2]. La simetría tetraédrica es otra duplicación de la simetría tetraédrica.

Las clases de conjugación de la simetría tetraédrica completa, T_d≅S₄, son:

• La identidad
• 8 × rotación de 120°
• 3 × rotación de 180°
• 6 × reflexión en un plano a través de dos ejes de rotación
• 6 × rotorreflexión de 90°

Las clases de conjugación de simetría piritoédrica, T_h, incluyen las de T, con las dos clases de 4 combinadas, y cada una con inversión:

• La identidad
• 8 × rotación de 120°
• 3 × rotación de 180°
• La inversión
• 8 × rotorreflexión 60°
• 3 × reflexión en un plano

Las clases de conjugación del grupo octaédrico completo, O_h≅S₄ × C₂, son:

• La inversión
• 6 × rotorreflexión de 90°
• 8 × rotorreflexión de 60°
• 3 × reflexión en un plano perpendicular a un eje cuádruple
• 6 × reflexión en un plano perpendicular a un eje doble

Las clases de conjugación de simetría icosaédrica completa, I_h≅A₅ × C₂, incluyen también cada una con su inversión:

• La inversión
• 12 × rotorreflexión de 108°, orden 10
• 12 × rotorreflexión de 36°, orden 10
• 20 × rotorreflexión de 60°, orden 6
• 15 × reflexión, orden 2

Grupos poliédricos quirales

Grupos poliédricos quirales

Nombre (Orb.)	Notación de Coxeter	Orden	Estructura abstracta	Puntos de rotación #valencia	Diagramas
					Ortogonal	Estereográfico
T (332)	[3,3]+	12	A4	43 32
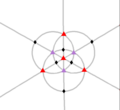
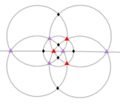
Th (3*2)	[4,3+]	24	A4×2	43 3*2
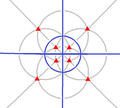
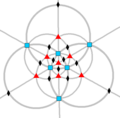
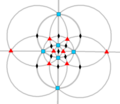
O (432)	[4,3]+	24	S4	34 43 62
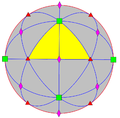
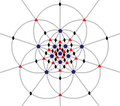
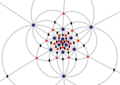
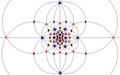
I (532)	[5,3]+	60	A5	65 103 152

Grupos poliédricos completos

Grupos poliédricos completos

Weyl Schoe. (Orb.)	Notación de Coxeter	Orden	Estructura abstracta	Número<br/>de Coxeter (h)	Planos especulares (m)	Diagramas especulares
						Ortogonal	Estereográfico
A3 Td (*332)	[3,3]	24	S4	4	6
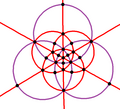
B3 Oh (*432)	[4,3]	48	S4×2	8	3 6
H3 Ih (*532)	[5,3]	120	A5×2	10	15

Véase también

• Símbolo de Wythoff
• Anexo:Grupos de simetría esférica

Referencias

Bibliografía

• Coxeter, H. S. M. Regular Polytopes, 3ra ed. Nueva York: Dover, 1973. ("The Polyhedral Groups". §3.5, pp. 46–47)

Enlaces externos

• Weisstein, Eric W. «PolyhedralGroup». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 

Esta página se editó por última vez el 10 nov 2023 a las 15:57.