Rectificación (geometría)

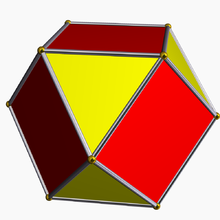
En geometría euclídea, la rectificación, también conocida como truncamiento crítico o truncamiento completo es el proceso de truncar un politopo marcando los puntos medios de todas sus aristas, y truncando sus vértices mediante planos que pasan por estos puntos.^[1]​ El nuevo politopo resultante estará delimitado por las facetas de las figuras de vértice y por las facetas una vez rectificadas del politopo original.

Un operador de rectificación a veces se denota con la letra r seguida de un símbolo de Schläfli. Por ejemplo, r{4,3} es el cubo rectificado, también llamado cuboctaedro, y también representado como ${\displaystyle {\begin{Bmatrix}4\\3\end{Bmatrix}}}$. Y un cuboctaedro rectificado rr{4,3} es un rombicuboctaedro, y también se representa como ${\displaystyle r{\begin{Bmatrix}4\\3\end{Bmatrix}}}$.

La notación de poliedros de Conway usa la letra ${\displaystyle a}$ para ambo como este operador. En teoría de grafos esta operación crea un grafo medial.

La rectificación de cualquier poliedro o teselado regular dual dará como resultado otro poliedro o teselado regular con un orden de teselado de 4. Por ejemplo, el tetraedro {3,3} se convierte en octaedro {3,4}. Como caso especial, un teselado cuadrado {4,4} se convertirá en otro teselado cuadrado {4,4} bajo una operación de rectificación.

Ejemplo de rectificación como truncamiento final a una arista

La rectificación es el punto final de un proceso de truncamiento. Por ejemplo, en un cubo, esta secuencia muestra cuatro pasos de un continuo de truncamientos entre la forma regular y la rectificada:

Rectificaciones de grado superior

La rectificación de mayor grado se puede realizar en politopos regulares de mayor dimensión. El mayor grado de rectificación crea el poliedro conjugado. Una rectificación trunca los bordes hasta convertirlos en puntos. Una birrectificación trunca caras hasta convertirlas en puntos. Una trirrectificación trunca las celdas reduciéndolas a puntos, y así sucesivamente.

Ejemplo de birrectificación como truncamiento final a una cara

Esta secuencia muestra un cubo birrectificado como la secuencia final de un cubo al dual donde las caras originales se truncan en un solo punto:

En polígonos

El dual de un polígono es lo mismo que su forma rectificada. Los nuevos vértices se colocan en el centro de los bordes del polígono original.

En poliedros y teselados planos

Cada sólido platónico y su conjugado tienen el mismo poliedro rectificado (aunque esto no es cierto para los politopos en dimensiones más altas).

El poliedro rectificado resulta expresable como la intersección del sólido platónico original con una versión concéntrica escalada apropiadamente de su dual. Por esta razón, su nombre es una combinación de los nombres del original y el dual:

1. El tetraedro rectificado, cuyo dual es el tetraedro, es el tetratetraedro, más conocido como octaedro.
2. El octaedro rectificado, cuyo dual es el cubo, es el cuboctaedro.
3. El icosaedro rectificado, cuyo dual es el dodecaedro, es el icosidodecaedro.
4. Un teselado cuadrado rectificado es también un teselado cuadrado.
5. Un teselado triangular o teselado hexagonal rectificado es un teselado trihexagonal.

Ejemplos

Familia	Original	Rectificado	Dual
[p,q]
[3,3]	Tetraedro	Octahedron	Tetraedro
[4,3]	Cubo	Cuboctaedro	Octaedro
[5,3]	Dodecaedro	Icosidodecaedro	Icosaedro
[6,3]	Teselado hexagonal	Teselado trihexagonal	Teselado triangular
[7,3]	Teselado heptagonal de orden-3	Teselado triheptagonal	Teselado triangular de orden-7
[4,4]	Teselado cuadrado	Teselado cuadrado	Teselado cuadrado
[5,4]	Teselado pentagonal de orden-4	Teselado tetrapentagonal	Teselado cuadrado de orden-5

En poliedros no regulares

Si un poliedro no es regular, los puntos medios de las aristas que rodean un vértice pueden no ser coplanares. Sin embargo, todavía es posible una forma de rectificación en este caso: cada poliedro tiene un grafo poliédrico como su 1-esqueleto, y a partir de ese gráfico se puede formar el grafo medial colocando un vértice en cada borde del punto medio del gráfico original y conectando dos de estos nuevos vértices por una arista siempre que pertenezcan a aristas consecutivas en una cara común. El gráfico medial resultante sigue siendo poliédrico, por lo que mediante el teorema de Steinitz se puede representar como un poliedro.

El equivalente en la notación de poliedros de Conway a rectificación es ambo, representado por la letra a. Aplicar dos veces aa, (rectificar una rectificación) es la operación denominada expansión de Conway, e, que es la misma que la operación canteado de Johnson, t_0,2 generada a partir de poliedros y teselados regulares.

En 4-politopos y teselaciones de panales 3D

Cada 4-politopo regular convexo tiene una forma rectificada como 4-politopo uniforme.

Un 4-politopo regular {p, q, r} tiene celdas {p, q}. Su rectificación tendrá dos tipos de celdas, un poliedro {p,q} rectificado que queda de las celdas originales y un poliedro {q,r} como nuevas celdas formadas por cada vértice truncado.

Sin embargo, una {p,q,r} rectificada no es lo mismo que una {r,q,p} rectificada. Otro truncamiento, llamado bitruncamiento, es simétrico entre un 4-politopo y su dual.

Ejemplos

Familía	Original	Rectificado	Birrectificado (Dual rectificado)	Trirectificado (Dual)
[p,q,r]	{p,q,r}	r{p,q,r}	2r{p,q,r}	3r{p,q,r}
[3,3,3]	Pentácoron	5-celdas rectificado	5-celdas rectificado	Pentácoron
[4,3,3]	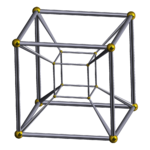Teseracto	Teseracto rectificado	16-celdas rectificado (Icositetracoron)	Hexadecacoron
[3,4,3]	icositetracoron	24-celdas rectificado	24-celdas rectificado	Icositetracoron
[5,3,3]	Hecatonicosacoron	120-celdas rectificado	600-celdas rectificado	Hexacosicoron
[4,3,4]	Panal cúbico	Panal cúbico rectificado	Panal cúbico rectificado	Panal cúbico
[5,3,4]	Dodecaédrico de orden-4	Dodecaédrico de orden-4 rectificado	Cúbico de orden-5 rectificado	Cúbico de orden-5

Grados de rectificación

Una primera rectificación trunca los bordes hasta convertirlos en puntos. Si un politopo es regular, esta forma se representa mediante una notación de símbolos de Schläfli extendida t₁{p,q,...} o r{p,q,...}.

Una segunda rectificación, o birrectificación, trunca caras en puntos. Si es regular tiene la notación t₂{p,q,...} o 2r{p,q,...}. Para poliedros, una birrectificación crea un poliedro conjugado.

Se pueden construir rectificaciones de mayor grado para politopos de mayor dimensión. En general, una n-rectificación trunca n-caras a puntos.

Si un n-politopo se rectifica a un estado (n-1), sus facetas se reducen a puntos y el politopo se convierte en su conjugado.

Notaciones y facetas

Hay diferentes notaciones equivalentes para cada grado de rectificación. Estas tablas muestran los nombres por dimensión y los dos tipos de facetas para cada uno.

Polígonos regulares

Las facetas son aristas, representadas como {2}.

Nombre {p}	Diagrama de Coxeter	Notación-t Símbolo de Schläfli	Símbolo de Schläfli vertical
			Nombre	Faceta-1	Faceta-2
Original		t0{p}	{p}	{2}
Rectificado		t1{p}	{p}		{2}

Poliedros y teselados regulares

Las facetas son polígonos regulares.

Nombre {p,q}	Diagrama de Coxeter	Notación-t Símbolo de Schläfli	Símbolo de Schläfli vertical
			Nombre	Faceta-1	Faceta-2
Original	=	t0{p,q}	{p,q}	{p}
Rectificado	=	t1{p,q}	r{p,q}= ${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$	{p}	{q}
Birrectificado	=	t2{p,q}	{q,p}		{q}

4-politopos uniformes regulares y panales regulares

Las facetas son poliedros regulares o rectificados.

name {p,q,r}	Diagrama de Coxeter	Notación-t Símbolo de Schläfli	Símbolo de Schläfli extendido
			Nombre	Faceta-1	Faceta-2
Original		t0{p,q,r}	{p,q,r}	{p,q}
Rectificado		t1{p,q,r}	${\displaystyle {\begin{Bmatrix}p\ \ \\q,r\end{Bmatrix}}}$= r{p,q,r}	${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$= r{p,q}	{q,r}
Birrectificado (Dual rectificado)		t2{p,q,r}	${\displaystyle {\begin{Bmatrix}q,p\\r\ \ \end{Bmatrix}}}$= r{r,q,p}	{q,r}	${\displaystyle {\begin{Bmatrix}q\\r\end{Bmatrix}}}$= r{q,r}
Trirrectificado (Dual)		t3{p,q,r}	{r,q,p}		{r,q}

5-politopos regulares y panales 4-espaciales regulares

Las facetas son 4 politopos regulares o rectificados.

name {p,q,r,s}	Diagrama de Coxeter	Notación-t Símbolo de Schläfli	Símbolo de Schläfli extendido
			Nombre	Faceta-1	Faceta-2
Original		t0{p,q,r,s}	{p,q,r,s}	{p,q,r}
Rectificado		t1{p,q,r,s}	${\displaystyle {\begin{Bmatrix}p\ \ \ \ \ \\q,r,s\end{Bmatrix}}}$= r{p,q,r,s}	${\displaystyle {\begin{Bmatrix}p\ \ \\q,r\end{Bmatrix}}}$= r{p,q,r}	{q,r,s}
Birrectificado (Dual birrectificado)		t2{p,q,r,s}	${\displaystyle {\begin{Bmatrix}q,p\\r,s\end{Bmatrix}}}$= 2r{p,q,r,s}	${\displaystyle {\begin{Bmatrix}q,p\\r\ \ \end{Bmatrix}}}$= r{r,q,p}	${\displaystyle {\begin{Bmatrix}q\ \ \\r,s\end{Bmatrix}}}$= r{q,r,s}
Trirrectificado (Dual rectificado)		t3{p,q,r,s}	${\displaystyle {\begin{Bmatrix}r,q,p\\s\ \ \ \ \ \end{Bmatrix}}}$= r{s,r,q,p}	{r,q,p}	${\displaystyle {\begin{Bmatrix}r,q\\s\ \ \end{Bmatrix}}}$= r{s,r,q}
Cuatrirrectificado (Dual)		t4{p,q,r,s}	{s,r,q,p}		{s,r,q}

Véase también

• Portal:Matemática. Contenido relacionado con Matemática.
• Portal:Geometría. Contenido relacionado con Geometría.
• Poliedro conjugado
• Poliedro quasirregular
• Anexo:Politopos regulares
• Truncamiento (geometría)
• Notación de poliedros de Conway

Referencias

Bibliografía

• Coxeter, H.S.M. Regular Polytopes, (3.ª edición, 1973), edición de Dover, ISBN 0-486-61480-8 (págs. 145–154 Capítulo 8: Truncamiento)
• Norman Johnson Polítopos Uniformes, Manuscrito (1991)
  • N.W. Johnson: La Teoría de los Politopos y Panales Uniformes, Ph.D. Disertación, Universidad de Toronto, 1966
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, Las simetrías de las cosas 2008, ISBN 978-1-56881-220-5 (Capítulo 26)

Enlaces externos

• Olshevsky, George. "Rectification". Glossary for Hyperspace.

Operadores de poliedros

Semilla	Truncamiento	Rectificación	Bitruncamiento	Dual	Expansión	Omnitruncamiento	Alternaciones
t0{p,q} {p,q}	t01{p,q} t{p,q}	t1{p,q} r{p,q}	t12{p,q} 2t{p,q}	t2{p,q} 2r{p,q}	t02{p,q} rr{p,q}	t012{p,q} tr{p,q}	ht0{p,q} h{q,p}	ht12{p,q} s{q,p}	ht012{p,q} sr{p,q}

Esta página se editó por última vez el 24 sep 2023 a las 11:26.